Finite Element Modeling for the Simulation of the Quasi-Static Compression of Corrugated Tapered Tubes

Summary

This protocol describes the study of the quasi-static compression performance of corrugated tapered tubes using finite element simulations. The influence of the thickness gradient on the compression performance was investigated. The results show that proper thickness gradient design can change the deformation mode and significantly improve the energy absorption performance of the tubes.

Abstract

In this study, the quasi-static compression performance of tapered tubes was investigated using finite element simulations. Previous studies have shown that a thickness gradient can reduce the initial peak force and that lateral corrugation can increase the energy absorption performance. Therefore, two kinds of lateral corrugated tapered tubes with variable thicknesses were designed, and their deformation patterns, load displacement curves, and energy absorption performance were analyzed. The results showed that when the thickness variation factor (k) was 0.9, 1.2, and 1.5, the deformation mode of the single corrugated tapered tube (ST) changed from transverse expansion and contraction to axial progressive folding. In addition, the thickness gradient design improved the energy absorption performance of the ST. The energy absorption (EA) and specific energy absorption (SEA) of the model with k = 1.5 increased by 53.6% and 52.4%, respectively, compared with the ST model with k = 0. The EA and SEA of the double corrugated tapered tube (DT) increased by 373% and 95.7%, respectively, compared with the conical tube. The increase in the k value resulted in a significant decrease in the peak crushing force of the tubes and an increase in the crushing force efficiency.

Introduction

Crashworthiness is an essential issue for lightweight automobiles, and thin-walled structures are widely used to improve crashworthiness. Typical thin-walled structures, such as round tubes, have good energy absorption capacity but usually have large peak forces and load fluctuations during the crushing process. This problem can be solved by introducing axial corrugations^1,2,3. The presence of corrugations allows the tube to plastically deform and fold according to a predesigned corrugation pattern, which can reduce the peak force and load fluctuations^4,5. However, this stable and controlled deformation pattern has a drawback: the energy absorption performance decreases. To improve the energy absorption of axial corrugated tubes, researchers have tried many methods, such as using a functional gradient design in the wavelength^6,7 and amplitude⁸, using filling foam^9,10, forming multichamber and multiwall structures¹¹, and forming combined tubes¹².

In addition, researchers have designed lateral corrugated tubes by introducing corrugations into the cross-section of circular tubes^13,14,15,16. The existence of lateral corrugations greatly improves the energy absorption performance of the tube^17,18,19. Eyvazian et al.²⁰ compared the crashworthiness of lateral corrugated tubes and ordinary circular tubes and showed that lateral corrugated tubes had a better energy absorption capacity. One reason for this observation is that the lateral corrugation strengthens the tube wall, which makes it more resistant to plastic folding. In addition, the corrugated wall of the plastic folding part flattens, and this flattening also absorbs energy. However, the high initial peak force is a disadvantage of this type of tube, and this high initial force may seriously affect the safety of the passengers being transported.

Functionally graded structures have a natural advantage in reducing the peak force. Common functionally graded thin-walled tubes are usually formed by changing the geometric parameters (e.g., the diameter and wall thickness)²¹. The most prevalent structures for which the diameter is changed are tapered tubes, including circular tapered tubes²², square tapered tubes^23,24,25, polygonal tapered tubes^26,27, axial corrugated tapered tubes^28,29,30, and tapered tubes with elliptical cross sections³¹. However, there are few studies on lateral corrugated tubes. Typical thickness gradient structures include square tubes^32,33, circular tubes^34,35, tapered tubes³⁶, multicellular tubes^37,38, and lattice structures³⁹. Deng et al.⁴⁰ reduced the initial peak force of lateral corrugated tubes with a thickness gradient design by 44.53%, but there have been no studies on lateral corrugated tapered tubes.

Although experiments are the most accurate and direct method to evaluate the crashworthiness of structures, they also require considerable money and resources. In addition, some important data, such as the stress-strain clouds of the structure and the energy values of different forms, are difficult to obtain in experiments¹⁸. Finite element analysis is a method to simulate the real load conditions by using mathematical approximation. This was first applied in the aerospace field, mainly for solving linear structural problems. Later, it was gradually applied to solve nonlinear problems in many fields, such as civil engineering, mechanical engineering, and material processing³⁴. In addition, with finite element software development, simulation results have become increasingly close to those of the corresponding experiments. Therefore, simulation using finite element analysis is used to investigate the crashworthiness of the structures. In this study, finite element analysis of the quasi-static compression performance of corrugated tapered tubes was conducted. The energy absorption of two types of lateral corrugated tapered tubes (i.e., the single corrugated tapered tube [ST] and the double corrugated tapered tube [DT]) with variable thicknesses was studied numerically. The results were compared with those obtained for a conventional conical tube (CT). The dimensions of the three types of thin-walled tubes are shown in Figure 1A. The geometric parameters of the ST are shown in Figure 1B, and the DT is built by crossing two STs. The thickness gradient is designed as shown in Figure 1C, and the thickness variation is defined by introducing a variation: factor k. In Figure 1C, t_h/2 = 0.44 mm, and k is set to 0, 0.3, 0.6, 0.9, 1.2, and 1.5. The results show that the peak crushing force decreases and the crushing force efficiency increases with increases in k.

Protocol

1. Creating the surface in the CAD software

1. Open the CAD software (see Table of Materials), left-click on File, left-click on New, and select Part.
2. In Part1, right-click on Top, and select Show.
3. Create a new plane: Press Ctrl, and left-click to select the Top plane and drag it up. Enter 30 mm as the Offset Distance, and rename the plane "Bottom".
4. Create a sketch on the "Top" plane.
   1. Right-click on Top, and select Sketch to create Sketch 1. Select Equation Driven Curve in Spline of the Sketch.
   2. Select Parametric in Equation Type. Input the parameters according to Table 1.
      NOTE: The sketch shape of the top plane is generated in this step. For example, if one desires to create a CT, enter 7.21 x sin(t), 7.21 x cos(t), 0 and 2 x pi in Table 1 in this step.
5. Create a sketch on the "Bottom" plane.
   1. Right-click on Bottom, and select Sketch to create Sketch 2. Select Equation Driven Curve in Spline.
   2. Select Parametric in Equation Type. Input the parameters according to Table 1.
      NOTE: The sketch shape of the bottom plane is generated in this step. For example, if you want to create a CT, enter 12.5 x sin(t), 12.5 x cos(t), 0, and 2 x pi in Table 1 in this step.
6. Generate the surface.
   1. Left-click on Lofted surface. Select Sketch 1 and Sketch 2 in Profiles, and select OK (see Supplementary File 1).
7. Repeat the above steps (steps 1.1-1.6) to generate three kinds of surfaces (Figure 1A), and name them CT, ST, and DT, as shown in Figure 1A.
   NOTE: Step 1.4.4 and step 1.5.4 create the sketches of the top and bottom planes, respectively, and step 1.6 connects the sketches of the top and bottom planes together to form a surface. The difference between the three planes is in the sketch of step 1.4.4 and step 1.5.4.

2. Building the model in the finite element software

NOTE: The quasi-static compression model of ST with k = 0.9 is described here as an example. The finite element models of the three types of tubes are exactly the same. Therefore, the different types of tubes in step 2.1.1 are to be imported, and step 2 needs to be repeated to get all the results.

1. Parts: Import and create the parts.
   1. Open the finite element software (see Table of Materials). Import the part "ST": left click File > Import > Part in order.Select the file ST, and name this part "ST" (see Supplementary File 2).
   2. Create the part "Bottom Plane": Left-click on Create Part. Under Shape, select Shell, name this part "Bottom Plane", and left-click on Continue. Select Create Circle: Center and Perimeter, and draw a circle with the origin as the center and a radius of 20 mm. Add the reference point set4 to the part "Bottom Plane".
   3. Create the part "Top Plane": Left-click on Create Part. Under Shape, select Shell, name this part "Top Plane", and left-click on Continue. Select Create Circle: Center and Perimeter, and draw a circle with the origin as the center and a radius of 20 mm.Add the reference point set5 to the part "Top Plane".
2. Property: Define the materialproperties, and assign the material to the section.
   1. Create the material properties.
      NOTE: The three types of tubes have the same material properties.
      1. Left-click on Create Material > General > Density in order,and enter "7.85E-09 (7.85 x 10⁻⁹)" under "Mass Density".
         NOTE: The material properties are obtained from previously published reports⁴¹ with the same materials, and an introduction to the materials is included in the discussion section.
      2. Left-click on Mechanical > Elasticity > Elastic in order, and under Young's Modulus and Poisson's Ratio, input "185,000" and "0.3", respectively.
      3. Left-click on Mechanical > Plasticity > Plastic in order, and enter the data taken from Figure 2 in "Yield Stress" and "Plastic Strain".
   2. Assign the section.
      1. Left-click on Create Section, under "Category", select Shell, and left-click on Continue.
      2. Under "Shell Thickness" select Nodal Distribution, left-click on Create Analytical Field, select Expression field, and enter the formula "0.44 − 0.9/100 x (Y − 15)".
         NOTE: The formula is used to change the thickness of the tube in the height direction and achieve the thickness gradient. The thickness variation factor k is defined as shown in Figure 1C, which indicates the thickness variation per unit height. In addition, the thickness of half of the height is set to a fixed value (i.e., t_h/2 = 0.44 mm) so that the thickness of the other heights can be derived from the middle height:
         0.44 − k/100 × (Y − 15)
         where Y is the height direction in the software.
      3. Left-click on Assign Section, pick ST from the interface, left-click on Done, and left-click on OK.
3. Assembly: Assemble the parts into a whole.
   1. Left-click on Create Instance, and select ST, Bottom Plane, and Top Plane. Then, left-click on OK | Rotate Instance, and select Bottom Plane and Top Plane. Enter the start point (0, 0, 0) and end point (1, 0, 0) of the rotation axis in turn, and enter 90 under Angle of Rotation. Left-click on Translate Instance, select Top Plane, and enter the start point (0, 0, 0) and end point (0, 30, 0) of the translation vector in turn.
4. Step: Create an analysis step, and set the history output items.
   1. Left-click on Create Step, select Dynamic, Explicit, and left-click on Continue. Under Time Period enter 0.05, and left-click on OK. Left-click on Create History Output, and select Energy.
   2. Left-click on Create History Output; under "Domain" select Set5, under "Output Variables" enter "RF2, U2", and left-click on OK.
5. Interaction: Set the contact properties and type, and set the top plane and bottom plane as rigid bodies.
   1. Left-click on Create Interaction Property, and select Contact. Under "Mechanical" select Tangential Behavior, under "Friction formulation" select Penalty, and under "Friction Coeff" enter "0.2".
   2. Left-click on Create Interaction, select General Contact (Explicit), and under "Global property assignment" select intProp-1.
   3. Left-click on Create Constraint, under "Type" select Rigid body, and pick up Bottom Plane and Top Plane.
6. Load: Fix the bottom plane, and set a downward loading speed of 500 mm/s on the top plane.
   1. Left-click on Create Boundary Condition, under "Types for Selected Step" select Displacement/Rotation, pick up set4, and enter 0 in all directions .
   2. Left-click on Create Boundary Condition, under "Types for Selected Step" select Velocity/Angular Velocity, pick up set5, enter −500 under "V2", and enter 0 in the other direction.
7. Mesh: Meshing and determining the element types.
   NOTE: Step 2.7 is important in the finite element analysis. The structure meshes into a finite number of elements, a suitable mathematical approximation solution is assumed for each element, and then the equilibrium conditions for the whole structure are derived and solved to obtain the solution to the problem.
   1. Left-click on Seed Part, enter 0.8 under "Approximate Global Size", and enter 0.08 under "By Absolute Value". Left-click on Mesh Part, and select Yes.
   2. Left-click on Assign Element Type, pick up the part, and select Done. Under "Element Library" select Explicit, and left-click on OK.
   3. Repeat step 2.7 to mesh the three parts CT, ST, and DT.The finite element model of the ST is shown in Figure 3.
8. Job: Submit the calculations, and export the results.
   1. Left-click on Create Job, select the model to calculate, and left-click on Continue. Left-click on Job Manager, select the model to calculate, and left-click on Submit.
   2. Select the completed model for calculation, and left-click on Results to enter the Visualization. The deformation mode of the ST (k = 0.9) is obtained from the Visualization. Left-click on Create XY Date. Select ODB history output, and click on Plot to plot the force-displacement curve of the ST (k = 0.9).
9. In step 2, step 2.1.1 has three structural choices, and step 2.2.2.2 has six choices of thickness variation factor (k), while the other steps are the same. Therefore, repeat the above steps 18 times to obtain the deformation modes and force-displacement curves for 18 models, as shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8. In addition, the crashworthiness evaluation indicators are obtained from the force-displacement curve through Equations 1-4, as shown in Figure 9, Figure 10, Figure 11 and Table 2.
   NOTE: The introduction of the crashworthiness evaluation indicators and Equations 1-4 are in the representative results.

Results

Several commonly used indicators are used to determine the crashworthiness of structures, including the total energy absorption (EA), specific energy absorption (SEA), peak crushing force (PCF), mean crushing force (MCF), and crushing force efficiency (CFE)⁴².

The total energy absorption (EA)⁴³ can be expressed as follows:

  ...

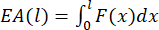Discussion

The quasi-static compression performance of tapered tubes was studied by finite element analysis. Two new types of corrugated tapered tubes with variable thicknesses were designed, and their quasi-static compression performance was investigated. In quasi-static compression simulations, some important steps and settings need to be verified.

The material parameters are the basic requirements for the finite element calculation (step 2.2.1 of the protocol). In this study, the material parameters w...

Materials

Name	Company	Catalog Number	Comments
ABAQUS	Dassault SIMULIA	Finite element software
CT	Botong 3D printing	Conical tube for experiment
SOLIDWORKS	Dassault Systemes	CAD software
Universal testing machine	SUNS	UTM5205, 200kN