A subscription to JoVE is required to view this content. Sign in or start your free trial.

In This Article

  • Summary
  • Abstract
  • Introduction
  • Protocol
  • Results
  • Discussion
  • Disclosures
  • Acknowledgements
  • Materials
  • References
  • Reprints and Permissions

Summary

Nuclear magnetic resonance (NMR) spectroscopy can characterize structural protein dynamics in a residue-specific manner. We provide a hands-on protocol for recording NMR 15N R1 and R2 relaxation and {1H}-15N heteronuclear Overhauser effect (hetNOE) experiments, sensitive to the picoseconds to nanoseconds timescale.

Abstract

Nuclear magnetic resonance (NMR) spectroscopy allows studying proteins in solution and under physiological temperatures. Frequently, either the amide groups of the protein backbone or the methyl groups in side chains are used as reporters of structural dynamics in proteins. A structural dynamics study of the protein backbone of globular proteins on 15N labeled and fully protonated samples usually works well for proteins with a molecular weight of up to 50 kDa. When side chain deuteration in combination with transverse relaxation optimized spectroscopy (TROSY) is applied, this limit can be extended up to 200 kDa for globular proteins and up to 1 MDa when the focus is on the side chains. When intrinsically disordered proteins (IDPs) or proteins with intrinsically disordered regions (IDRs) are investigated, these weight limitations do not apply but can go well beyond. The reason is that IDPs or IDRs, characterized by high internal flexibility, are frequently dynamically decoupled. Various NMR methods offer atomic-resolution insights into structural protein dynamics across a wide range of time scales, from picoseconds up to hours. Standard 15N relaxation measurements overview a protein's internal flexibility and characterize the protein backbone dynamics experienced on the fast pico- to nanosecond timescale. This article presents a hands-on protocol for setting up and recording NMR 15N R1, R2, and heteronuclear Overhauser effect (hetNOE) experiments. We show exemplary data and explain how to interpret them simply qualitatively before any more sophisticated analysis.

Introduction

The function of a protein is determined not only by its three-dimensional structure but also by its structural dynamics, encompassing its internal flexibility and structural transitions between different conformations the protein will adopt. Nuclear magnetic resonance (NMR) spectroscopy can investigate the structural dynamics of proteins in solution1,2,3. Recent developments in proton-detected solid-state NMR also allow for the characterization of protein dynamics in a less soluble state, such as, e.g., a lipid bilayer membrane4,5,6. In solution NMR, the structural dynamics of the protein backbone and protein side chains can be studied. For a globular protein, a structural dynamics study of the protein backbone can be achieved up to 50 kDa once the protein is 15N isotopically labeled. When side chain deuteration and transverse relaxation optimized spectroscopy (TROSY) are employed, this limit can be extended up to 200 kDa7,8. When the focus lies on side-chain dynamics, the range of accessible proteins and complexes can be extended up to 1 MDa2,9.

The named weight limitations do not apply to intrinsically disordered proteins (IDPs), which frequently show high intrinsic dynamics. Over 30% of the eukaryotic proteome comprises IDPs or intrinsically disordered regions (IDRs)10,11,12,13. They play central roles in many cellular processes, such as signal transduction and transcription1, and are frequently involved in intracellular phase separation14,15,16,17. IDPs lack a well-defined three-dimensional (3D) native structure under physiological conditions and have a weakly funneled or rugged energy landscape17,18. Due to a low hydrophobicity and strong electrostatic repulsion distributed over the backbone of IDPs or IDRs, a driving force for folding to a rigid structure is missing19. IDPs frequently adopt a folded conformation when complex with other binding partners10,20,21. Also, post-translational modifications (PTMs) expand the folding possibilities of IDPs or IDRs22,23. Misfolding of IDPs has been identified as a cause of various diseases, including neurodegenerative diseases15,24,25,26.

IDPs and IDRs show high internal flexibility21,27,28. Conformational ensembles displaying the variation of atomic positions and dihedral angles were derived from molecular dynamics simulations and restraints obtained from experimental data29,30,31,32. Due to dynamics and resulting disorder in the frozen state, the diffuse electron density makes it difficult to structurally characterize them using state-of-the-art methods in structural biology, such as cryo-EM or X-ray crystallography. Also, crystallization conditions or sample preparation techniques for experiments at cryogenic temperatures may impact the conformational space experienced by IDPs. However, the solution NMR works well for highly dynamic proteins and is therefore well-suited for investigating IDPs16,20,22,28,29,30,31,32,33,34,35,36,37,38.

As introduced above, solution NMR offers various techniques to study internal protein dynamics across a wide range of time scales (Figure 1), primarily based on spin relaxation31,33,38,39,40,41,42.

Spin relaxation of the 15N nuclei in the amide groups of the protein backbone is induced by 1H-15N bond angle orientation changes due to internal protein dynamics and collective motions (including, when relevant, rotational diffusion)27,43,44,45,46,47,48,49,50,51. At timescales shorter than the rotational correlation time τR (the time the molecule needs to rotate one radiant, also dubbed overall tumbling correlation time), the chemical shift anisotropy (CSA) and the dipolar coupling (D) are active and not averaged by the rotational diffusion of the protein. Internal dynamics of the protein backbone, comprising variations in bond angles, reorientations of bonds, and rotational tumbling, induce stochastic fluctuations of the CSA and dipolar coupling tensor, resulting in a variation of the local magnetic field, ultimately leading to NMR spin relaxation47,48,52,53. These fluctuations can be described by an overall correlation function. The Fourier transform of the overall correlation function is called the spectral density function. In the semi-classical Redfield relaxation theory, the NMR relaxation rate constants can be described by linear combinations of these spectral density functions54.

Backbone 15N NMR relaxation experiments developed in the early 1990s comprise 15N R1, R1ρ, and {1H}-15N nuclear Overhauser effect experiments, sensitive to the fast picosecond (ps) nanosecond (ns) timescale, faster than the rotational correlation time τR of the protein45,55,56,57. To characterize backbone dynamics slower than the rotational correlation time τR, so-called relaxation dispersion experiments, R1ρ, and Carr-Purcell-Meiboom-Gill (CPMG) experiments sensitive to microsecond (µs) - millisecond (ms) dynamics44,46,58,59,60,61 are used. Dynamics slower than microseconds can be captured by 15N chemical exchange saturation transfer (CEST) NMR62, exchange spectroscopy (EXSY, milliseconds to seconds), or Real-time (RT) NMR (seconds to hours)63,64. The PRE (paramagnetic relaxation enhancement) effect of paramagnetic probes, as well as residual dipolar couplings (RDCs), can be used to assess the entire range of ps to ms dynamics65,66,67,68.

figure-introduction-8677
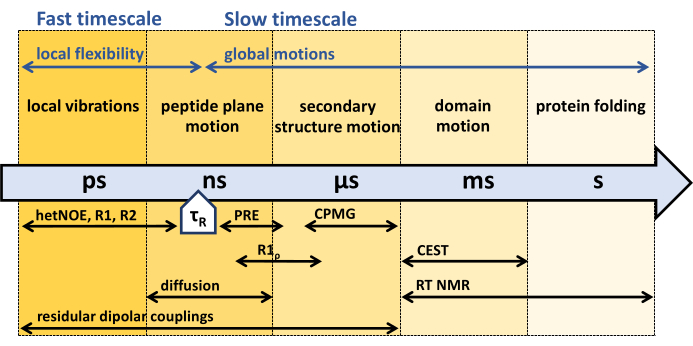
Figure 1: Time scales of protein backbone dynamics and sensitive time window of different NMR dynamics experiments. NMR offers a variety of methods to characterize protein backbone dynamics across a wide range of timescales. Different motions experienced by the protein backbone are indicated at their respective timescales. The protein's rotational correlation time, τR, is the time the protein needs for an overall rotation (by one radiant). Motions faster than the protein's rotational correlation time, τR, can be associated with the protein's internal flexibility. Various NMR experiments and their sensitivity to the respective timescales are indicated below the arrow. Please click here to view a larger version of this figure.

The protocol below describes the setup of NMR relaxation experiments by Lakomek et al.69 and Stief et al.70, using a sensitivity-enhanced heteronuclear single quantum coherence (HSQC) detection scheme. Before proceeding to the experimental implementation, a very brief overview of NMR spin relaxation and NMR relaxation experiments is given. Due to size restraints and to keep this protocol comprehensible, this overview must remain simplistic (and therefore incomplete).

The longitudinal or spin-lattice relaxation, characterized by the T1 time or the R1 = 1/ T1 rate constant, describes the return of magnetization to Boltzmann equilibrium. In equilibrium, the magnetization is aligned along the axis of the outer magnetic field, which defines the z-axis of the laboratory frame. Spectral densities at high (1H) and small (15N) Larmor frequencies (the NMR resonance frequencies, e.g., 600 MHz for 1H for a 14.1 Tesla magnet) and linear combinations of these Larmor frequencies contribute to the 15N R1 relaxation, which is characterized by the 15N R1 rate constants measured in rad·s-1. Motions on timescales are inverse to these Larmor frequencies; thus, motions on the picosecond to nanosecond timescale contribute to the relaxation rate constant R1. For molecules that show overall tumbling and where a rotational correlation time can be defined, the R1 (T1) curve shows a maximum (minimum) for ωτR = 1, with the rotational correlation τR and the Larmor frequency ω of the spin under consideration. If multiple Larmor frequencies contribute, the one with the lowest frequency is the dominant one, e.g., ωN in the case of 15N R1. The fast motion regime (ωτR much smaller than 1) applies to small molecules that tumble very fast and for low magnetic fields and low viscosity. The slow motion regime (ωτR much larger than 1) is valid for larger molecules that tumble slower and for high magnetic fields and high viscosity.

Globular folded proteins show overall tumbling in solution, and a rotational correlation time can be assigned. However, the concept of overall tumbling is no longer valid for intrinsically disordered proteins and frequently differs from assigning a single rotational correlation time. Here, the residue-specific internal correlation time becomes more critical.

The described pulse sequence measuring 15N R1 relaxation rates (Figure 2) is based on a sensitivity-enhanced HSQC read-out experiment with an Echo/ Anti-Echo detection for quadrature detection69,70,71. Short gradients with variable strength and length are used for coherence selection and improved water suppression70. During that time, 15N longitudinal polarization will relax. Longer decay times lead to reduced intensities in the associated 2D planes of this pseudo-3D spectrum (delay data points are recorded in the third dimension). A loop element, described below, is executed an increasing number of times for longer relaxation times. As cross-correlated relaxation between the 15N chemical shift anisotropy (CSA) and the 1H and 15N dipolar coupling (D) is also active during the relaxation delay, a central I-BURP-2 180° pulse72, selective on the amide protons, is necessary to refocus the contribution by cross-correlated relaxation (which if not refocused would lead to skewed and erroneous 15N R1 rate constants).

figure-introduction-13785
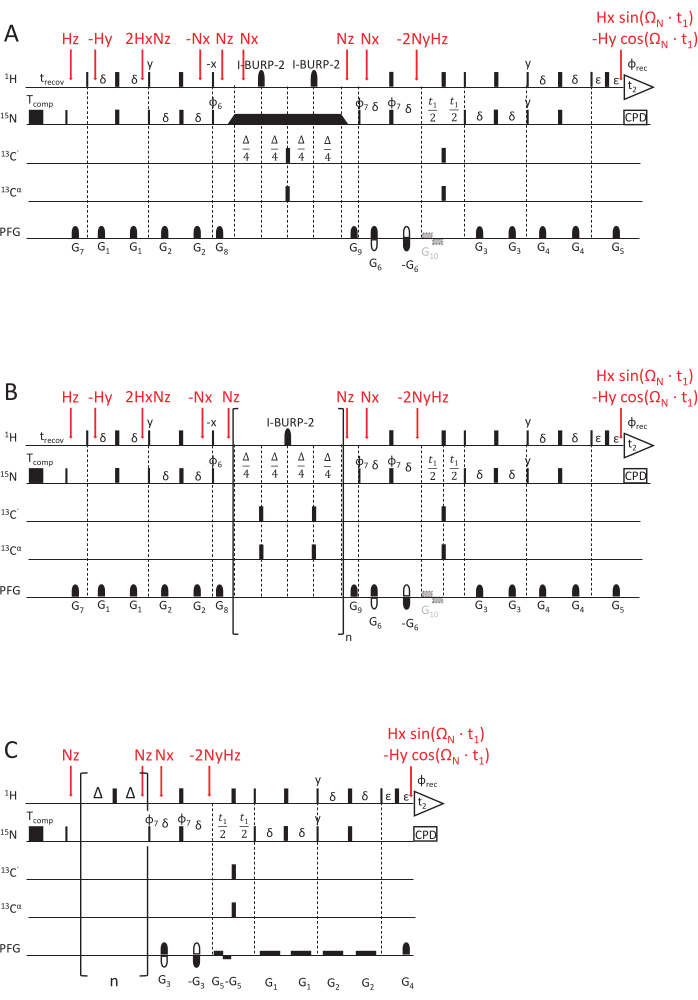
Figure 2: NMR pulse sequence schemes for determining the NMR relaxation rate constants. (A) 15N R1ρ, (B) 15N R1, and (C) hetNOE experiment, using a sensitivity-enhanced HSQC read-out scheme69,70. 90°(x) pulses are visualized by narrow rectangles and 180°(x) pulses by wide rectangles, unless indicated otherwise. The following phase cycle is applied: φ6 = y, y, -y, -y; φ7 = y, -y, φrec = y, -y, -y, y. Quadrature detection is achieved by inverting the polarity of gradient G5 and the phase cycle of φ7 (Echo/ Anti-Echo detection). (A) 15N R1ρ experiment: The black rectangular represents the spin-lock, for which the duration varies to acquire different relaxation delays. The triangles before and after the spin-lock indicate the adiabatic shape pulses that align the magnetization along the effective magnetic field axis Beff. G10 is an optional gradient to prevent radiation damping of the water magnetization during the evolution phase. (B) 15N R1 experiment: The bracketed part shows the sequence's loop element, repeated an n number of times to match the desired relaxation delay. (C) The hetNOE pulse scheme is similar to the second half of R1 and R1ρ pulse schemes, namely the t1 evolution time and HSQC-detection element. However, 15N magnetization is excited directly without any INEPT. Saturation of the proton magnetization (to achieve cross-relaxation between 1H and 15N) is achieved by a train of 180(1H) pulses applied for at least 5 s. An idle delay of the same lengths (here, 5 s) without any pulse train is applied for the reference experiment. G5 is an optional gradient to prevent radiation damping, and the inversion in polarity of gradient G4, in combination with phase φ7 = y, -y, -y, y, achieves quadrature detection. The magnetization transfer steps, represented by product operators, are marked in red. Please click here to view a larger version of this figure.

The relaxation rate constant R2 describes the relaxation of transverse polarization (in the xy-plane orthogonal to the external magnetic field) due to loss of phase coherence between the spin, leading to decay of detectable magnetization53,54. The spectral density function at high and small frequencies contributes to R2, similar to R1. However, the biggest contribution to R2 originates from the spectral density at zero frequency. For this reason, R2 is very sensitive to the rotational tumbling, described by the rotational correlation time τR, which is in the order of a few ns for a small globular protein at room temperature. Thus, slower backbone motions in the hundreds of ps to low ns regime contribute the most. Exchange dynamics of the backbone that cause a modulation of the isotropic part of the chemical shift tensor of the 15N nuclei, in principle, add an exchange contribution R2ex to the R2 rate constants43,44,49,60,61. In the described experiments, the R2ex contribution is suppressed by a spin-lock that refocuses dynamics slower than the inverse circular frequency of the spin-lock. The spin-lock is a long continuous wave radiofrequency pulse that keeps the magnetization aligned along the effective magnetic field axis Beff (the vector sum of the spin-lock ω1 field and the chemical shift offset from the 15N carrier frequency (see below)). The relaxation of the magnetization aligned along the B1,eff axis is called R1ρ relaxation, which has a R1 component and a R2 component. Using formula (1), R2 can be calculated from R1ρ and R144,73:

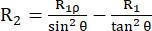figure-introduction-18493 (1).

The angle between the axis of the effective magnetic field Beff and the external magnetic field B0 is 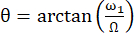figure-introduction-18741. ω1 is the RF amplitude of the spin-lock and Ω the chemical shift offset between the 15N chemical shift of the corresponding residue and the 15N carrier frequency 44,73.

The R1ρ pulse scheme (Figure 2A, 70) is very similar to the 15N R1 scheme except for the relaxation delay. To measure the 15N R1ρ relaxation rates, the spin-lock must be active after the magnetization has been aligned along the effective field axis Beff by an adiabatic pulse with the same radio-frequency (RF) amplitude as the spin-lock. The length of the spin-lock will be varied to obtain the different relaxation delays.

The steady-state {1H}-15N nuclear Overhauser effect (1H-15N NOE), dubbed hetNOE in the following, is the ratio of the cross-relaxation rate and the 15N longitudinal relaxation rate. It leads to a reduction of the steady-state polarization on 15N due to cross-relaxation with the proton upon saturation of the proton polarization45,53,54,74,75. The cross-relaxation depends on spectral density functions of the sum and difference of the 1H and 15N Larmor frequencies. Therefore, the hetNOE is sensitive both to fast picosecond dynamics (< 100 ps) and also to ps-ns dynamics (due to its R1 dependence). The sequence69 (Figure 2C) is based on a sensitivity-enhanced HSQC read-out with Echo/ Anti-Echo gradients for quadrature detection. For saturation of the proton magnetization and the resulting hetNOE, the equilibrium proton magnetization is inverted and subsequently saturated by rapidly pulsing 180° pulses for about 5 times the 15 N T1. For the reference experiment, the recovery delay is equal to the saturation delay but without the 1H 180°pulse train. An extra delay of D1 = 2 s is added for the reference experiment and the one with 1H saturation. Both experiments are recorded back-to-back and differ only in applying 1H 180°pulses (saturation) or not (reference). The ratio of spectral intensities recorded in the experiment with 1H saturation divided by the intensities of the reference experiment (without the 180° proton pulse train) gives the {1H}-15N NOE (hetNOE) value.

The following protocol describes the setup of NMR relaxation experiments by Lakomek et al.69 and Stief et al.70. We focus on NMR pulse sequences using a sensitivity-enhanced HSQC detection scheme. The 15N R1 and R1ρ experiments are implemented as described in detail by Stief et al.70, and the hetNOE experiment is described by Lakomek et al.69.

Protocol

1. NMR sample preparation

NOTE: Isotope labeling of the proteins is performed for higher-dimensional NMR and advanced NMR experiments. When protein expression in E. coli and protein purification had been established using rich media (e.g., Luria-Bertani [LB] or 2x yeast extract tryptone medium [2YT]) with a yield of several milligrams per liter, preparing an isotopically labeled NMR sample is usually relatively straightforward.

  1. For isotope labeling, use M9 minimal media for gene expression, where 15N ammonium chloride is the only nitrogen source and 13C-enriched glucose is the only carbon source.
  2. For protein purification, follow the standard protocol established in the laboratory for the respective protein.
    ​NOTE: The results section shows representative results for an IDP, the monomeric SNARE protein Synaptobrevin-2 (1-96). NMR isotope labeling of Synaptobrevin-2 has been performed as described in70. For very high-precision measurements, using low D2O concentrations, less than 5%, is recommended. This is because of the deuterium isotope effect, which can be observed in Hahn-Echo 15N T2 and at low-frequency 15N CPMG relaxation dispersion experiments (not discussed here) but has only a minimal impact in 15N R1ρ experiments (where it is primarily refocused)76.

2. Preparations for running the NMR relaxation experiments on the spectrometer

NOTE: The described NMR relaxation experiments are specific for Bruker spectrometers. They have been tested on cryogenic and room temperature 1H, 15N, and 13C triple resonance probes and Avance III and Avance Neo consoles operated by the Bruker software Topsin 3.6 or higher.

  1. Follow the precautions.
    1. Do a safety briefing before working at the NMR spectrometer.
    2. Check the probe's power specifications of the used spectrometer and choose an appropriate pulse length and pulse power for every pulse, e.g., by comparing consistency with the Topspin "prosol" table entries.
  2. Import the pulse sequences.
    1. Download the NMR pulse programs either from the website indicated below or from the extended Biological Magnetic Resonance Bank (BMRB) repository (bmrbig102) to the directory /opt/topspin4.1.4/exp/stan/nmr/lists/pp/user of the computer operating the NMR spectrometer. Please adjust the topspin version (here: topspin4.1.4 to the respective version installed on the spectrometer).
    2. Download the NMR-shaped pulses either from the website indicated below or from the extended Biological Magnetic Resonance Bank (BMRB) repository (bmrbig102) to the directory /opt/topspin4.1.4/exp/stan/nmr/lists/pp/user of the computer operating the NMR spectrometer. Please adjust the topspin version (here: topspin 4.1.4 to the respective version installed on the spectrometer).
  3. Calibrate the spectrometer and sample.
    1. Set the temperature of interest. For temperature calibration, apply the facility's protocols. For example, use a Methanol-d4 sample and interpret the observed chemical shift difference using the web application NMR thermometer (https://chem.ch.huji.ac.il/nmr/software/thermometer.html); see also77.
    2. Insert the sample (plus an additional 5% D2O for the lock) and wait approximately 10 min to allow the sample to equilibrate its temperature. Lock the deuterium (2H) signal (command: lock, select H2O+D2O).
    3. Match and tune the 1H, 15N, and 13C channels, e.g., using the atma or atmm routine. If no automatic matching and tuning unit is installed, manually match and tune the probe using the wobb command.
    4. Perform shimming for a homogenous B0 field, e.g., using the topshim routine tg.
  4. Calibrate the 90° (1H) pulse length.
    1. Use the zg experiment. Use getprosol to import the probe parameters. Choose a short duration of 5 µs for P1. Check and correct the specified power level of the probe for PLW1 if needed.
    2. Start the experiment with zg. Process the data with efp. Adjust the phase with .ph so that the baseline is even and the NMR signal of the water resonance is in phase.
    3. Estimate a 360° (1H) pulse by taking a common or approximate 90° (1H) pulse (e.g., from the listed spectrometer specifications) and multiplying it by a factor of four. Run the experiment and process it.
      NOTE: The chosen duration is too long if the signal is positive and too short if negative. The 360° (1H) pulse will be the zero crossing.
    4. Adjust the pulse length accordingly. Do this iteratively to find the zero crossing. Divide the obtained value by four. That will be the 90° (1H) pulse.
      NOTE: An alternative to the described 360° method is the pulscal routine, which can be started from the command line and allows an automated 1H pulse calibration.
  5. Calibrate the carrier frequency O1 to the water resonance.
    1. Copy the zg experiment by typing edc in the command line to a new experiment number. Type rpar to open the parameter sets (Supplementary Figure 1A).
    2. Search for the parameter set ZGPR. Click on the parameter set ZGPR (Supplementary Figure 1A), click on Read, choose Execute "getprosol" and click OK (Supplementary Figure 1B).
    3. Change P1 to the calibrated 90° (1H) pulse length. Choose a saturation length of D1 = 2 s and a pulse power of PLW9 of 50 dB. Set the receiver gain (rg) to 16. Alternatively, execute the receiver gain adjustment by typing rga and setting the receiver gain to the specified value (But avoid "receiver gain overflow").
    4. Type gs in the command line to start for a repeated, continuous acquisition. Go to the acquisition window and change the O1 to reduce the FID area dominated by the water signal (Supplementary Figure 2).
    5. Click below the marker to decrease the O1, and click above the marker to increase it. Use the sensitivity button to change the step size. Save the current O1; Close stops the repeated acquisition (Supplementary Figure 2).
  6. Calibrate the 90° (15N) pulse length.
    1. Copy the zg experiment to a new experiment number (type edc). Type rpar to read the parameter set HSQCFPF3GPPHWG to change the pulse program to a 1H-15N HSQC experiment. Use the option Keep parameters P1, O1, and PLW1 (Supplementary Figure 1).
    2. Type getprosol 1H <calibrated 90° (1H) pulse length in µs> <90° (1H) pulse strength in db> in the command line to import the probe parameters. Set the number of scans (NS) to 8 and the dummy scans (DS) to 2.
      NOTE: < > specifies here the values to be set. For example: getprosol 1H 8.5 -11.79.
    3. Run the first increment of the experiment by typing zg in the command line. Copy the first increment to a new experiment number with rser 1 <new experiment number>. Process the data with efp and phase the spectrum with .ph. Use the first increment (1D experiment) of the experiment for the following steps.
      NOTE: The < > specify the chosen number for the new experiment, e.g., rser 1 101.
    4. Type ased in the command line to open the pulse sequence parameters of the 1D experiment. Click on the E in the PULPROG line (see Supplementary Figure 3A) to open the pulse program editor.
    5. Use the following workflow to save the pulse sequence under a new name: Click File (left upper corner), Save as, enter the new name, and click OK. Then click Set PULPROG to the dataset (see Supplementary Figure 3B) and click OK.
    6. Modify the original 1H-15N HSQC sequence (saved under a new name, see 2.6.4.) by multiplying the 90° (15N) after the t1 evolution period (before the back transfer) by a factor of 2 (the 90° (15N) pulse is now 180° (15N)). Press Ctrl S to save the pulse sequence. Set the pulse length to 90° (15N) (P21) so that the NMR signal of the first increment will vanish (at the zero crossing) (Supplementary Figure 3B).
    7. Open the 1H-15N HSQC experiment (2D experiment) and enter the calibrated 90° (15N) pulse length (P21). Type getprosol 1H <calibrated 90° (1H) pulse length in µs> <90° (1H) pulse strength in db> 15N <calibrated 90° (15N) pulse length in µs> <90° (15N) pulse strength in db> in the command line.
  7. Determine the spectral widths and appropriation of acquisition times.
    1. In the acquisition parameter window for the 1H-15N HSQC experiment (type eda in the command line), adjust the spectral width (acquisition parameter SW) and the number of dimension increments in direct and indirect dimensions (acquisition parameter TD).
      1. Choose for SW, 16 ppm in the direct (1H) and 30 ppm in the indirect (15N) dimension. Choose for TD, 2048 in the direct (1H) and 512 in the indirect (15N) dimension.
    2. Acquire the 1H-15N HSQC experiment.
      1. Check that all signals of interest are detected and that no aliasing artifacts are present in the spectrum. Change the O3P if the center of the spectrum does not fit with the center of the protein signal distribution along the 15N axis.
      2. Increase the SW if the spectral window is too small. Increase the TD to gain a higher FID resolution (Check the probe specifications for the maximum duration of decoupling).
        NOTE: This is the general setup and the starting point for the setup of NMR relaxation experiments. It is recommended to record the 1H-15N HSQC experiment at the beginning and end of the entire set of experiments and, for more extended experimental times, also in between to monitor sample integrity.

3. Implementing the NMR relaxation experiments

NOTE: The NMR relaxation pulse sequences (Figure 2) are available at https://www.ipb.hhu.de/en/teams/team-lakomek/pulsesequences  or at the extended Biological Magnetic Resonance Bank (BMRB) repository (bmrbig102).

  1. Set up the 15N R1ρ experiment.
    1. Copy the HSQC experiment (type edc) to a new directory. Type ased and change the pulse program to the 15N R1ρ experiment by clicking on the three dots of the parameter line PULPROG in the pulse sequence parameters (ased, see Supplementary Figure 3A). Double-click on the pulse program, click on Set PULPROG to dataset (see Supplementary Figure 3B), and click OK.
      NOTE: Some error messages may appear. Close these messages.
    2. Type gpnam in the command line to insert all missing gradient shapes (gpnam1- gpnam9) as described in the pulse sequence (Supplementary Figure 4).
    3. Type vplist in the command line. Click on the three dots (Supplementary Figure 5A), File (upper left corner), and New (Supplementary Figure 5B).
    4. Type a name for a new dummy vplist, and press OK. Create the dummy vplist (5m, 65m, 25m, 45m, 15m, 55m, 35m, 10m; a new row for each vplist entry). Press Ctrl S to save the list and close the window of the vplist (Supplementary Figure 5C).
    5. Double-click on the name of the newly created vplist (Supplementary Figure 5B).
      NOTE: This is necessary to avoid compilation errors in the pulse sequence. The appropriate entries of the vplist will be determined further below (point 3.1.29.).
    6. Type ased to open the pulse sequence parameters (Supplementary Figure 6). Enter all missing gradient strengths and gradient lengths as given in the pulse sequence (Supplementary Figure 6D).
    7. Enter for the loop counter L3 (number of complex points in the indirect dimension) 1/2 of the 15N TD entry in the acquisition parameter window (eda). Enter for the loop counter L6 the number of recorded relaxation data points used for fitting the relaxation curve.
      NOTE: This number L6 corresponds to the number of vplist entries, here: 8 (Supplementary Figure 6A).
    8. Set the adiabatic TanhTan_half.nl pulse, downloaded from the website specified above, as the shape of the 15N SP8 pulse. Set the adiabatic TanhTan_2nd.nl pulse from the website as the shape of the 15N SP9 pulse (Supplementary Figure 6C).
    9. Set the P8 entry to the length of the adiabatic TanhTan pulse - sufficiently long to guarantee the adiabaticity of the pulse; here P8 = 3000 µs is chosen (Supplementary Figure 6C).
    10. Set the 15N decoupling (CPDPRG 3) to a garp decoupling scheme. Use for the length of decoupling PCPD3 200 µs (Supplementary Figure 6C).
    11. Set the interscan recovery delay to at least D1 = 2 s or longer.
      NOTE: For the choice of a proper recovery delay, see the Discussion section.
    12. Set the dummy scans (DS) to at least 64 for the final experiment (during the setup, DS = 4 is sufficient for time reasons). As a starting point, use a number of scans (NS) of 4; use multiples of 4 if the signal-to-noise (SNR) is too low (Supplementary Figure 6A).
    13. Set the O1 to the calibrated carrier frequency of step 2.5. Set the O2P to 176 ppm and copy the O3P from the 1H-15N HSQC experiment (Supplementary Figure 6A-C).
    14. Set the pulse length P7 to the 90° (15N) pulse length calibrated in step 2.6. Also, copy the pulse power level of the 90° (15N) pulse from step 2.6 to PLW3 and PLW7 (Supplementary Figure 6C).
    15. Set the pulse length P1 and P19 to the 90° (1H) pulse length calculated in step 2.4. (Supplementary Figure 6B).
    16. Set the number of increments in the indirect dimension TD = l3 * 2 * l6 (eda or type td in the command line).
      NOTE: All pulse sequence parameters described here are additionally annotated in the pulse sequence.
    17. Set the shape pulse SP5 to an I-BURP2 shape (Iburp2.1000). Set the pulse length P15 to 2000 µs. Open the shape tool display by clicking on the E next to the I-BURP2 shape pulse in the Topspin pulse sequence parameter window (ased) (Supplementary Figure 6B).
    18. Simulate the shape pulse with the correct length by clicking the Start NMR Simulation button. Check the shaped pulse length [µs] (= 2000 µs) and the rotation angle [°] (= 180°) in the simulation window. Click on Start NMR-SIM (Supplementary Figure 7A).
    19. Check the excitation range and choose the appropriate I-BURP2 pulse length to cover the protein's 1H spectral dispersion but avoid excitation of the water at the same time. Set P15 to the Shaped pulse length of the simulation window with the best IBURP-2 pulse simulated (Supplementary Figure 7B).
      NOTE: The proper length is chosen if the I-BURP2 excites (> 95% effectiveness) the entire amide region. To simulate an I-BURP2 pulse with a different length, close the excitation profile window and edit the shaped pulse length in the simulation window. Click on Start NMR-SIM. Pulses with a shorter length have a broader excitation range in Hz.
    20. Set SPOFFS5 to change the carrier frequency of the I-BURP2 pulse and shift the excitation range to the left or right to avoid the I-BURP2 pulse touching and disturbing the water magnetization (Supplementary Figure 6B).
    21. To determine the appropriate power level of the shaped pulse, open the Bruker shape tool, click the Start NMR Simulation button, and set the I-BURP2 pulse length to Shaped pulse length [µs]. Remember the corresponding length of a soft rectangular 90° (1H) pulse, visible in the simulation window at the corresponding 90° square pulse [µs] (Supplementary Figure 7A).
    22. Type calcpowlev. Use the hard 90° (1H) pulse (P1) in microseconds as the reference length (Supplementary Figure 8B) and the 90° (1H) soft rectangular pulse corresponding to the I-BURP2 pulse in microseconds as the new length (Supplementary Figure 8A). Remember the power difference Δ in dB between the hard 90° (1H) pulse and the soft rectangular pulse (Supplementary Figure 8C). Copy the pulse strength of the hard 90° (1H) pulse in dB to SPW5 and add the memorized difference Δ in dB (Supplementary Figure 6B).
    23. To determine the power level of the spin-lock, calculate the corresponding 90° (15N) pulse length of the spin-lock. Use the formula: 90° (15N) pulse length in s = 0.25 / (spin-lock power in Hz).
    24. Use calcpowlev to calculate the power difference Δ in dB between the power of the spin-lock and the 90° (15N) hard pulse (P7). New: 90° (15N) pulse length of the spin-lock in µs (Supplementary Figure 8A). Ref: hard 90° (15N) pulse length in µs (Supplementary Figure 8B). Copy the power level PLW7 of the 90° (15N) hard pulse in dB to the spin-lock power level PLW8 (Supplementary Figure 6C), and add the calculated power difference Δ in dB (Supplementary Figure 8C).
    25. Copy the power level of the spin-lock PLW8 to the power levels SPW8 and SPW9. (Supplementary Figure 6C).
    26. To determine the power level of the 15N decoupling, use calcpowlev to calculate the power difference Δ between the power of the 90° (15N) decoupling pulse (PCPD3) and the 90° (15N) hard pulse (P7). New: PCPD3 in µs (200) (Supplementary Figure 8A). Ref: hard 90° (15N) pulse length in µs (Supplementary Figure 8B). Copy the power level PLW7 of the 90° (15N) hard pulse in dB to the decoupling level PLW31 (Supplementary Figure 6C) and add Δ in dB (Supplementary Figure 8C).
    27. To use temperature compensation, include #define TEMP_COMPENSATION (by deleting the semicolon in the pulse sequence). Set P18 to the maximum duration of the spin-lock used in the 15N R1ρ experiment.
      NOTE: Switching off the temperature compensation for the first trial of the experiment is recommended.
    28. In the case of 15N 13C labeled samples, include # to define LABEL_CN in the pulse program (by deleting the semicolon in the pulse sequence). Set P4 to the pulse length calculated with the formula in78. For example, it corresponds to 23.70 µs at 600 MHz and 11.85 µs at 1200 MHz. Type calcpowlev to calculate the power difference in dB between P4 and the (13C) hard pulse. Copy the (13C) hard pulse power in dB to PLW4 and add the Δ in dB. Copy PLW4 to PLW2 (Supplementary Figure 6B).
    29. Determine the relaxation delays for appropriate sampling.
      1. Run the first eight FIDs (in case L6 = 8) and process these (rser <number of FID> < new experiment number>). Choose the entries in the vplist that the peak intensity of the experiment with the longest delay decreases to at least 1/e (approx. 37%), but not less than 25% compared to the experiment with the shortest delay (which serves as the reference).
      2. Adjust the remaining entries of the vplist to achieve an even sampling of the intensity decreases between the FID with the longest delay and the FID with the shortest delay. Read the NOTE and the power specifications of the probe.
        NOTE: The slowly relaxing residues will dominate the first FID. Adjust the remaining entries of the vplist to achieve an even sampling of the intensity decreases between the first and second FID. Do not exceed the probe's maximum allowed spin-lock power and length (consult probe manual and probe specifications). In case of temperature compensation, check P18 (maximum spin-lock duration), as the overall spin-lock duration of P18 will be applied, split between the relaxation delay and temperature compensation. It holds time (relaxation delay) + time (temperature compensation) = const = P18. For a 2 kHz spin-lock, we prefer not to exceed a spin-lock duration of more than 65 ms, using a recovery delay (D1) of 2 s. In that case, a compromise between the maximum spin-lock duration and the longest relaxation delay must be taken in favor of the maximum allowed spin-lock duration. In case of longer D1 recovery delays, longer spin-lock powers may be applicable. What counts is the overall power deposition in the probe over time. If longer spin-lock durations are required, only increase the spin-lock lengths in small steps and watch the lock signal. As a rule of thumb, adjust the lock level in the upper third of your lock display. If the lock level reduces by more than two squares during the execution of the pulse sequence, the spin-lock power deposited in the probe is too much.
    30. Type rga in the command line to determine the receiver gain. For a good signal-to-noise ratio, aim for a receiver gain (rg) value between 128 and 256, which proves good water suppression.
      NOTE: A receiver gain between 128 and 256 cannot be reached indicates a too-strong water signal. In that case, the gradient power and durations are gently adjusted until the receiver gain is reached. See also the Discussion section.
    31. Start a test run of the 15N R1ρ experiment by typing zg in the command line. Check that the water signal is well suppressed for all delays (1 to 8, in case of 8 delays in the vplist). Check also increment 9, which is the second increment of the quadrature detection scheme (Echo/ Anti-Echo).
  2. Set up the 15N R1 experiment.
    1. Copy the 15N R1ρ experiment and change the pulse program to the 15N R1 experiment.
    2. Type vclist, generate a vclist, and enter the dummy vclist described in70: 0, 24, 6, 20, 4, 16, 8, 12; a new row for each vclist entry).
    3. Open ased. Check the gradient lengths and strengths. Change GPZ9 to 14%.
    4. Check pulse lengths, pulse shapes, and pulse strengths (the correct values should have been copied from the 15N R1ρ experiment).
    5. In the case of 15N13C labeled samples, use #define LABEL_CN in the pulse program.
    6. For the use of temperature compensation, include #define TEMP_COMPENSATION.
    7. Run the first eight FIDs (in case L6 = 8) and process these (rser <number of FID> < new experiment number>). Choose the entries in the vclist that the peak intensity of the experiment with the longest delay decreases to at least 1/e (approx. 37%) but not less than 25% compared to the experiment with the shortest delay. Adjust the remaining entries of the vplist to achieve an even sampling of the intensity decreases between the FID with the longest delay and the FID with the shortest delay.
      NOTE: Only even numbers are allowed for vclist entries.
  3. Set up the {1H}-15N NOE experiment.
    1. Copy the 15N R1 relaxation experiment and change the pulse sequence to the {1H}-15N NOE pulse scheme.
    2. Set the length of the saturation period with the loop counter L8. The spacing between 180° (1H) pulses is 22 ms79 (2* 1 / JNH). To achieve the most accurate results, use a saturation period of about 5 times the protein's 15N T1(15N). Here: 5 s. That would correspond to L8 = 230.
      NOTE: The Discussion section provides additional advice on choosing the saturation period/recovery delay.
    3. Change the length and strength of the gradients as described in the pulse scheme. Use sine.20 gradient shapes.
    4. Set the number of increments in the indirect dimension equal to TD = l3 * 2 * 2
    5. In the case of 15N13C labeled samples, use #define LABEL_CN and -DLABEL_CN as a ZGOPTNS.
    6. Run the pulse schemes by typing zg in the command line.

4. Processing and analysis of the recorded NMR experiments

NOTE: Spectra have been recorded using a Bruker system. Processing is performed using a Unix or Linux operating system. Spectra processing and data analysis were performed using NMRPipe80 and python3. The NMRPipe software can be downloaded at https://www.ibbr.umd.edu/nmrpipe/index.html. NMRPipe-based processing scripts are downloaded from the website: https://www.ipb.hhu.de/en/teams/team-lakomek/pulsesequences or from the extended Biological Magnetic Resonance Bank (BMRB) repository (bmrbig102). It is recommended to use NMRPipe. If NMRPipe is not available or desired, alternatives such as CCPN81 or SPARKY (SPARKY 3, or its successors NMRFAM-SPARKY82 or POKY83 ) can be used.

  1. Process and analyze 15N R1 experiment.
    NOTE: The following commands are executed in a Unix Terminal.
    1. Copy the files in the downloaded directory R1_processing to the directory containing the experimental R1 data (working directory).
    2. Make the files executable by the terminal command: > chmod u+x *.com
    3. Execute > bruker to open the NMRPipe Conversion Utility and generate the fid.com file. Click Read Parameters. Change the Dimension Count to two if three dimensions are counted, and click Read Parameters again. Then click Clear Script, Update Script, and Save Script (Supplementary Figure 9).
      NOTE: If the carrier frequency is not correct, change the Center Position PPM after clicking Read Parameters the second time.
    4. Execute > ./fid.com
    5. Convert the vclist in a vplist with ms entries: delay in ms = 40 ms * entry of vclist. Use > cp vclist vplist and edit the vplist.
    6. Use > ./split.com to split the pseudo 3D data into eight 2D files.
    7. Edit the tauValues (vplist values in order of the vplist) and the idxExpmt values (order of tauValues regarding the time) in nmrproc.com (Supplementary Figure 10).
    8. Use > ./nmrproc.com to process the raw data of all eight 2D spectra.
    9. Use > nmrDraw to draw the spectra.
      1. Use the reference spectrum (first entry in vplist) for these steps. Switch to that spectrum by changing the z dimension to one (upper left corner). Adjust the contour level using the + and - next to the Factor button. Redraw the spectrum with the button Draw.
      2. Use a contour level where all signals of interest can be recognized with only a few signals coming from the noise (the contour level is at the edge of the noise level) (Supplementary Figure 11).
    10. Correct the spectrum phase, type v for vertical 1D-signal projection and h for horizontal 1D-signal projection. Adjust the phase with P0 and P1 (Supplementary Figure 11), remember the phase difference, and correct the phase in the nmrproc.com file (Supplementary Figure 10).
      NOTE: If the spectrum is flipped in the 15N dimension, remove the -neg in the line: | nmrPipe -fn FT -neg \ (Supplementary Figure 10).
    11. Close nmrDraw and process again with > nmrproc.com. For Peak picking (after the spectrum is phased correctly and the reference spectrum is displayed with a contour level where all peaks are present), type K (shift + k), press Detect, and click on Save. (Supplementary Figure 11).
    12. Copy a peak list to the working directory and change -assName in ass.com to the name of the peak list (Supplementary Figure 12).
      NOTE: An example of a peaklist in the correct format is available at https://www.ipb.hhu.de/en/teams/team-lakomek/pulsesequences
      and at the extended Biological Magnetic Resonance Bank (BMRB) repository (bmrbig102).
    13. Execute > ./ass.com to assign the spectra. Verify the assignment that the script suggests for the various peaks. Use the left mouse button to assign and the right mouse button to deassign peaks. Use the Next button to go to the following amino acid and Prev to go to the previous amino acid (Supplementary Figure 13).
      NOTE: The contour level can be changed with + and - at the top right corner. Use the button Draw to redraw the spectrum with the new contour level (Supplementary Figure 13).
    14. After completing the assignment, click Save and then Save again. Afterward, click on Quit, Cancel, and Exit (Supplementary Figure 13).
    15. Execute > python3 NoneDeleter.py to create relax.tab, which contains only information on assigned peaks.
    16. Execute > ./relax.com to generate the autofit.com script.
    17. Execute > ./autoFit.com to perform a Fourier Interpolation and generate pseudo ratios of the different delay times for each amino acid (axt.tab and nlin.tab are generated).
    18. Execute > ./model.com to generate the modelExp.com script based on the data in nlin.tab.
    19. Execute > ./modelExp.com to fit the evolution curve of each residue with a non-linear Least-Squares Optimization model.
    20. Execute > bash summary.tcl -in relax.tab > t1.tab. Ignore a potential error message: GDB Notice: 21 missing values in the table file can occur.
    21. Copy t1.tab into a newly created directory R1R2.
  2. Process and analyze the 15N R1ρ experiment.
    1. Copy the files in the downloaded directory R1rho_processing to the directory containing the experimental R1ρ data (working directory).
    2. Execute > chmod u+x *.com
    3. Execute > bruker to open the NMRPipe Conversion Utility and generate the fid.com file. See also the processing of the 15N R1 spectra.
    4. Execute > ./fid.com
    5. Execute > ./split.com to split the pseudo 3D data into eight 2D files.
    6. Execute > ./nmrproc.com (Edit the tauValues [vplist values] and the idxExpmt beforehand) to process the raw data of all eight 2D spectra (Supplementary Figure 10).
    7. Execute > nmrDraw to draw the spectra and pick the peaks. Use the reference spectrum (first entry in vplist) for these steps. Follow the same procedure as for the 15N R1 experiment.
    8. Copy a peak list to the working directory and change -assName in ass.com to the name of the peak list (Supplementary Figure 12).
    9. Execute > ./ass.com and follow the same procedure as for the 15N R1 experiment.
    10. Execute > python3 NoneDeleter.py to create relax.tab, which contains only information on assigned peaks.
    11. Execute > ./relax.com
    12. Execute > ./autoFit.com
    13. Execute > ./model.com
    14. Execute > ./modelExp.com
    15. Execute > bash summary.tcl -in relax.tab > t1rho. tab. Ignore potential error message: GDB Notice: 21 missing values in the table file may occur.
    16. Copy the following header in the t1rho.tab file (the values can be obtained from the fid.com file) (Supplementary Figure 14):
      REMARK 600MHz for T1rho
      REMARK -yOBS = 60.818 (put here the value found in fid.com)
      ​REMARK -yCAR = 119.06 (put here the value found in fid.com)
    17. Execute > ./extract_PPM.com to generate a table called fusionOffset.tab that contains the offset of the peak 15N frequency relative to the carrier frequency (which will be needed to calculate the angle θ for the extraction of R2 data from the R1 and R1ρ data).
  3. Summarize the relaxation data.
    1. Copy the t1rho.tab and the fusionOffset.tab into the directory R1R2.
    2. Copy the script crtR1p.tcl in the directory R1R2, adjust the spectrometer frequency and spin-lock power, and execute bash crtR1p.tcl | sort -n > R1R2.tab. (Supplementary Figure 15). R1R2.tab will contain the fitted R1ρ rate constants, theta angle, R2 rate constants, and R1 rate constants.
  4. Process and analyze the hetNOE experiment.
    1. Copy the files in the downloaded directory NOE_processing to the experimental NOE data directory (working directory).
    2. Execute > chmod u+x *.com
    3. Execute > bruker to open the NMRPipe Conversion Utility and generate the fid.com file. Click Read Parameters. Change the Dimension Count to two if three dimensions were counted and press Read Parameters again. Then press Clear Script, Update Script, and Save Script.
    4. Execute > ./fid.com
    5. Execute > ./split.com (A vplist with two entries (0, 1) has to be created before)
    6. Execute > ./ft2.com
    7. Execute > nmrDraw to draw the spectrum and pick the peaks in the reference spectrum (z-dimension = 1). Extract and remember the noise (press T = shift + t). Phase correction and peak picking follow the same procedure as the 15N R1 experiment.
    8. Copy a peak list to the working directory and change -assName in ass.com to the name of the peak list (Supplementary Figure 12)
    9. Execute > ./ass.com to assign the spectra. Follow the same procedure as detailed for the 15N R1 experiment.
    10. Execute > python3 NoneDeleter.py to create relax.tab.
    11. Execute > ./script.com
    12. Execute > ./autoFit.com
    13. Change the noise in error_hetnoe.tcl.
    14. Execute > bash error_hetnoe.tcl |sort -n > hetNOE.tab

Results

The following shows some exemplary NMR relaxation data recorded on the vesicular SNARE protein Synaptobrevin-2 (1-96), frequently called VAMP2 (vesicle-associated protein 2). For recording the NMR data, we used a 171 µM 15N Synaptobrevin-2 (1-96) sample (dubbed Syb-2 in the following) in 50 mM MES (pH 6.0) buffer containing 150 mM NaCl, 0.1 mM TCEP, and 1 mM EDTA. All experimental data was recorded at 278.15 K using a 250 µL volume filled in a 3 mm NMR sample tube. Experiments were performed at a Bru...

Discussion

This protocol described the setup of NMR 15N relaxation experiments by Lakomek et al.69 and Stief et al.70. We focused on NMR pulse sequences using a sensitivity-enhanced HSQC detection scheme. The 15N R1 and R1ρ experiments are implemented as described in detail by Stief et al.70, and the hetNOE experiment is described by Lakomek et al.69.

When setti...

Disclosures

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

We thank Melinda Jaspert and Kevin Bochinsky for the helpful discussions. N.L. thanks the German Science Foundation for funding through the Heisenberg Program (DFG grant number 433700474). This work is further supported by the project "Virological and immunological determinants of COVID-19 pathogenesis - lessons to get prepared for future pandemics (KA1-Co-02 "COVIPA"), a grant from the Helmholtz Association's Initiative and Networking Fund. We acknowledge generous access to the Jülich-Düsseldorf Biomolecular NMR Center, jointly run by Forschungszentrum Jülich and Heinrich Heine University Düsseldorf (HHU).

Materials

NameCompanyCatalog NumberComments
Bruker 600 MHz AVANCE III HD spectrometer Brukerhttps://www.bruker.com/en/products-and-solutions/mr/nmr/avance-nmr-spectrometer.htmlNMR experiments conducted 

References

  1. Sekhar, A., Kay, L. E. An NMR view of protein dynamics in health and disease. Annu Rev Biophys. 48, 297-319 (2019).
  2. Rosenzweig, R., Kay, L. E. Bringing dynamic molecular machines into focus by methyl-TROSY NMR. Annu Rev Biochem. 83, 291-315 (2014).
  3. Palmer, A. G. Enzyme dynamics from NMR spectroscopy. Acc Chem Res. 48 (2), 457-465 (2015).
  4. Reif, B. Ultra-high resolution in MAS solid-state NMR of perdeuterated proteins: implications for structure and dynamics. J Magn Reson. 216, 1-12 (2012).
  5. Schanda, P., Ernst, M. Studying dynamics by magic-angle spinning solid-state NMR spectroscopy: Principles and applications to biomolecules. Prog Nucl Magn Reson Spectrosc. 96, 1-46 (2016).
  6. Le Marchand, T., et al. (1)H-H-detected biomolecular NMR under fast magic-angle spinning. Chem Rev. 122 (10), 9943-10018 (2022).
  7. Pervushin, K., Riek, R., Wider, G., Wuthrich, K. Attenuated T2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc Natl Acad Sci U S A. 94 (23), 12366-12371 (1997).
  8. Tzakos, A. G., Grace, C. R., Lukavsky, P. J., Riek, R. NMR techniques for very large proteins and RNAs in solution. Annu Rev Biophys Biomol Struct. 35, 319-342 (2006).
  9. Sprangers, R., Kay, L. E. Quantitative dynamics and binding studies of the 20S proteasome by NMR. Nature. 445 (7128), 618-622 (2007).
  10. Wright, P. E., Dyson, H. J. Intrinsically disordered proteins in cellular signalling and regulation. Nat Rev Mol Cell Biol. 16 (1), 18-29 (2015).
  11. van der Lee, R., et al. Classification of intrinsically disordered regions and proteins. Chem Rev. 114 (13), 6589-6631 (2014).
  12. Tompa, P. Intrinsically unstructured proteins. Trends Biochem Sci. 27 (10), 527-533 (2002).
  13. Dyson, H. J., Wright, P. E. Coupling of folding and binding for unstructured proteins. Curr Opin Struct Biol. 12 (1), 54-60 (2002).
  14. Uversky, V. N. Intrinsically disordered proteins in overcrowded milieu: Membrane-less organelles, phase separation, and intrinsic disorder. Current Opinion in Structural Biology. 44, 18-30 (2017).
  15. Patel, A., et al. A liquid-to-solid phase transition of the ALS protein FUS accelerated by disease mutation. Cell. 162 (5), 1066-1077 (2015).
  16. Abyzov, A., Blackledge, M., Zweckstetter, M. Conformational dynamics of intrinsically disordered proteins regulate biomolecular condensate chemistry. Chem Rev. 122 (6), 6719-6748 (2022).
  17. Uversky, V. N. Unusual biophysics of intrinsically disordered proteins. Biochim Biophys Acta. 1834 (5), 932-951 (2013).
  18. Papoian, G. A. Proteins with weakly funneled energy landscapes challenge the classical structure-function paradigm. Proc Natl Acad Sci U S A. 105 (38), 14237-14238 (2008).
  19. Uversky, V. N., Gillespie, J. R., Fink, A. L. Why are "natively unfolded" proteins unstructured under physiologic conditions. Proteins. 41 (3), 415-427 (2000).
  20. Bah, A., et al. Folding of an intrinsically disordered protein by phosphorylation as a regulatory switch. Nature. 519 (7541), 106-109 (2015).
  21. Tompa, P., Schad, E., Tantos, A., Kalmar, L. Intrinsically disordered proteins: emerging interaction specialists. Curr Opin Struct Biol. 35, 49-59 (2015).
  22. Dyson, H. J., Wright, P. E. Perspective: the essential role of NMR in the discovery and characterization of intrinsically disordered proteins. J Biomol NMR. 73 (12), 651-659 (2019).
  23. Adamski, W., et al. A unified description of intrinsically disordered protein dynamics under physiological conditions using NMR spectroscopy. J Am Chem Soc. 141 (44), 17817-17829 (2019).
  24. Dobson, C. M. Protein folding and misfolding. Nature. 426 (6968), 884-890 (2003).
  25. Bertoncini, C. W., et al. Release of long-range tertiary interactions potentiates aggregation of natively unstructured alpha-synuclein. Proc Natl Acad Sci U S A. 102 (5), 1430-1435 (2005).
  26. Buell, A. K., et al. Solution conditions determine the relative importance of nucleation and growth processes in alpha-synuclein aggregation. Proc Natl Acad Sci U S A. 111 (21), 7671-7676 (2014).
  27. Salvi, N., Abyzov, A., Blackledge, M. Atomic resolution conformational dynamics of intrinsically disordered proteins from NMR spin relaxation. Prog Nucl Magn Reson Spectrosc. 102, 43-60 (2017).
  28. Schneider, R., Blackledge, M., Jensen, M. R. Elucidating binding mechanisms and dynamics of intrinsically disordered protein complexes using NMR spectroscopy. Curr Opin Struct Biol. 54, 10-18 (2019).
  29. Rezaei-Ghaleh, N., Blackledge, M., Zweckstetter, M. Intrinsically disordered proteins: from sequence and conformational properties toward drug discovery. Chembiochem. 13 (7), 930-950 (2012).
  30. Jensen, M. R., Salmon, L., Nodet, G., Blackledge, M. Defining conformational ensembles of intrinsically disordered and partially folded proteins directly from chemical shifts. J Am Chem Soc. 132 (4), 1270-1272 (2010).
  31. Camacho-Zarco, A. R., et al. NMR provides unique insight into the functional dynamics and interactions of intrinsically disordered proteins. Chem Rev. 122 (10), 9331-9356 (2022).
  32. Mittag, T., Forman-Kay, J. D. Atomic-level characterization of disordered protein ensembles. Curr Opin Struct Biol. 17 (1), 3-14 (2007).
  33. Dyson, H. J., Wright, P. E. Unfolded proteins and protein folding studied by NMR. Chem Rev. 104 (8), 3607-3622 (2004).
  34. Dyson, H. J., Wright, P. E. NMR illuminates intrinsic disorder. Curr Opin Struct Biol. 70, 44-52 (2021).
  35. Sugase, K., Dyson, H. J., Wright, P. E. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature. 447 (7147), 1021-1025 (2007).
  36. Bessa, L. M., et al. The intrinsically disordered SARS-CoV-2 nucleoprotein in dynamic complex with its viral partner nsp3a. Sci Adv. 8 (3), eabm4034 (2022).
  37. Milles, S., Salvi, N., Blackledge, M., Jensen, M. R. Characterization of intrinsically disordered proteins and their dynamic complexes: From in vitro to cell-like environments. Prog Nucl Magn Reson Spectrosc. 109, 79-100 (2018).
  38. Salvi, N., Abyzov, A., Blackledge, M. Atomic resolution conformational dynamics of intrinsically disordered proteins from NMR spin relaxation. Prog Nucl Magn Reson Spectrosc. 102 - 103, 43-60 (2017).
  39. Gill, M. L., Byrd, R. A., Palmer, A. G. Dynamics of GCN4 facilitate DNA interaction: a model-free analysis of an intrinsically disordered region. Phys Chem Chem Phys. 18 (8), 5839-5849 (2016).
  40. Bertoncini, C. W., et al. Structural characterization of the intrinsically unfolded protein beta-synuclein, a natural negative regulator of alpha-synuclein aggregation. J Mol Biol. 372 (3), 708-722 (2007).
  41. Rezaei-Ghaleh, N., et al. Local and global dynamics in intrinsically disordered synuclein. Angew Chem Int Ed Engl. 57 (46), 15262-15266 (2018).
  42. Rezaei-Ghaleh, N., Parigi, G., Zweckstetter, M. Reorientational dynamics of amyloid-beta from NMR spin relaxation and molecular simulation. J Phys Chem Lett. 10 (12), 3369-3375 (2019).
  43. Palmer, A. G. NMR characterization of the dynamics of biomacromolecules. Chem Rev. 104 (8), 3623-3640 (2004).
  44. Palmer, A. G., Massi, F. Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem Rev. 106 (5), 1700-1719 (2006).
  45. Kay, L. E., Torchia, D. A., Bax, A. Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry. 28 (23), 8972-8979 (1989).
  46. Mittermaier, A., Kay, L. E. Review - New tools provide new insights in NMR studies of protein dynamics. Science. 312 (5771), 224-228 (2006).
  47. Abragam, A. . Principles of Nuclear Magnetism. , (1983).
  48. Ernst, R. R., Bodenhausen, G., Wokaun, A. . Principles of Nuclear Magnetic Resonance in One and Two Dimensions. , (1990).
  49. Cavanagh, J., Fairbrother, W. J., Palmer, A. G., Skelton, N. J. . Protein NMR Spectroscopy: Principles and Practice. , (1995).
  50. Levitt, M. H. . Spin Dynamics: Basics of Nuclear Magnetic Resonance. , (2008).
  51. Keeler, J. . Understanding NMR Spectroscopy. , (2010).
  52. Bloembergen, N., Purcell, E. M., Pound, R. V. Relaxation effects in nuclear magnetic resonance absorption. Phys Rev. 73 (7), 679-712 (1948).
  53. Wangsness, R. K., Bloch, F. The dynamical theory of nuclear induction. Phys Rev. 89 (4), 728-739 (1953).
  54. Redfield, A. G. On the theory of relaxation processes. IBM J Res Dev. 1 (1), 19-31 (1957).
  55. Peng, J. W., Wagner, G. Mapping of the spectral densities of N-H bond motions in eglin c using heteronuclear relaxation experiments. Biochemistry. 31 (36), 8571-8586 (1992).
  56. Farrow, N. A., et al. Backbone dynamics of a free and a phosphopeptide-complexed src homology-2 domain studied by n-15 NMR relaxation. Biochemistry. 33 (19), 5984-6003 (1994).
  57. Tolman, J. R., Ruan, K. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem Rev. 106 (5), 1720-1736 (2006).
  58. Mulder, F. A. A., Skrynnikov, N. R., Hon, B., Dahlquist, F. W., Kay, L. E. Measurement of slow (mu s-ms) time scale dynamics in protein side chains by N-15 relaxation dispersion NMR spectroscopy: Application to Asn and Gln residues in a cavity mutant of T4 lysozyme. J Am Chem Soc. 123 (5), 967-975 (2001).
  59. Tollinger, M., Skrynnikov, N. R., Mulder, F. A. A., Forman-Kay, J. D., Kay, L. E. Slow dynamics in folded and unfolded states of an SH3 domain. J Am Chem Soc. 123 (46), 11341-11352 (2001).
  60. Akke, M., Palmer, A. G. Monitoring macromolecular motions on microsecond to millisecond time scales by R(1)rho-R(1) constant relaxation time NMR spectroscopy. J Am Chem Soc. 118 (4), 911-912 (1996).
  61. Loria, J. P., Rance, M., Palmer, A. G. A relaxation-compensated Carr-Purcell-Meiboom-Gill sequence for characterizing chemical exchange by NMR spectroscopy. J Am Chem Soc. 121 (10), 2331-2332 (1999).
  62. Vallurupalli, P., Bouvignies, G., Kay, L. E. Studying "Invisible" excited protein states in slow exchange with a major state conformation. J Am Chem Soc. 134 (19), 8148-8161 (2012).
  63. Jeener, J., Meier, B. H., Bachmann, P., Ernst, R. R. Investigation of exchange processes by 2-dimensional NMR-spectroscopy. J Chem Phys. 71 (11), 4546-4553 (1979).
  64. Palmer, A. G., Kroenke, C. D., Loria, J. P. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzymol. 339, 204-238 (2001).
  65. Clore, G. M., Iwahara, J. Theory, practice, and applications of paramagnetic relaxation enhancement for the characterization of transient low-population states of biological macromolecules and their complexes. Chem Rev. 109 (9), 4108-4139 (2009).
  66. Iwahara, J., Clore, G. M. Detecting transient intermediates in macromolecular binding by paramagnetic NMR. Nature. 440 (7088), 1227-1230 (2006).
  67. Lakomek, N. A., et al. Residual dipolar couplings as a tool to study molecular recognition of ubiquitin. Biochem Soc Trans. 36 (Pt 6), 1433-1437 (2008).
  68. Johnson, C. N., Libich, D. S. Paramagnetic relaxation enhancement for detecting and characterizing self-associations of intrinsically disordered proteins. J Vis Exp. (175), e63057 (2021).
  69. Lakomek, N. A., Ying, J., Bax, A. Measurement of (1)(5)N relaxation rates in perdeuterated proteins by TROSY-based methods. J Biomol NMR. 53 (3), 209-221 (2012).
  70. Stief, T., Vormann, K., Lakomek, N. A. Sensitivity-enhanced NMR (15)N R(1) and R(1rho) relaxation experiments for the investigation of intrinsically disordered proteins at high magnetic fields. Methods. 223, 1-15 (2024).
  71. Kay, L. E., Keifer, P., Saarinen, T. Pure absorption gradient enhanced heteronuclear single quantum correlation spectroscopy with improved sensitivity. J Am Chem Soc. 114 (26), 10663-10665 (1992).
  72. Geen, H., Freeman, R. Band-selective radiofrequency pulses. J Magn Reson (1969). 93 (1), 93-141 (1991).
  73. Desvaux, H., Berthault, P. Study of dynamic processes in liquids using off-resonance RF irradiation. Prog Nucl Magn Reson Spectrosc. 35 (4), 295-340 (1999).
  74. Overhauser, A. W. Polarization of nuclei in metals. Phys Rev. 91 (2), 476-476 (1953).
  75. Overhauser, A. W. Polarization of nuclei in metals. Phys Rev. 92 (2), 411-415 (1953).
  76. Kumari, P., Frey, L., Sobol, A., Lakomek, N. A., Riek, R. (15)N transverse relaxation measurements for the characterization of micros-ms dynamics are deteriorated by the deuterium isotope effect on (15)N resulting from solvent exchange. J Biomol NMR. 72 (3-4), 125-137 (2018).
  77. Karschin, N., Krenek, S., Heyer, D., Griesinger, C. Extension and improvement of the methanol-d(4) NMR thermometer calibration. Magn Reson Chem. 60 (4), 203-209 (2022).
  78. Sattler, M., Schleucher, J., Griesinger, C. Heteronuclear multidimensional NMR experiments for the structure determination of proteins in solution employing pulsed field gradients. Prog Nucl Magn Reson Spectrosc. 34 (2), 93-158 (1999).
  79. Ferrage, F., Cowburn, D., Ghose, R. Accurate sampling of high-frequency motions in proteins by steady-state N-{H} nuclear Overhauser effect measurements in the presence of cross-correlated relaxation. J Am Chem Soc. 131 (17), 6048-6049 (2009).
  80. Delaglio, F., et al. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR. 6 (3), 277-293 (1995).
  81. Skinner, S. P., et al. CcpNmr AnalysisAssign: a flexible platform for integrated NMR analysis. J Biomol NMR. 66 (2), 111-124 (2016).
  82. Lee, W., Tonelli, M., Markley, J. L. NMRFAM-SPARKY: enhanced software for biomolecular NMR spectroscopy. Bioinformatics. 31 (8), 1325-1327 (2015).
  83. Lee, W., Rahimi, M., Lee, Y., Chiu, A. POKY: a software suite for multidimensional NMR and 3D structure calculation of biomolecules. Bioinformatics. 37 (18), 3041-3042 (2021).
  84. Abyzov, A., et al. Identification of dynamic modes in an intrinsically disordered protein using temperature-dependent NMR relaxation. J Am Chem Soc. 138 (19), 6240-6251 (2016).
  85. Singh, A., Purslow, J. A., Venditti, V. 15N CPMG relaxation dispersion for the investigation of protein conformational dynamics on the micros-ms timescale. J Vis Exp. (170), e62395 (2021).
  86. Gopalan, A. B., Hansen, D. F., Vallurupalli, P. CPMG experiments for protein minor conformer structure determination. Methods Mol Biol. 1688, 223-242 (2018).
  87. Tugarinov, V., Kay, L. E. Methyl groups as probes of structure and dynamics in NMR studies of high-molecular-weight proteins. Chembiochem. 6 (9), 1567-1577 (2005).
  88. Lipari, G., Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J Am Chem Soc. 104 (17), 4546-4559 (1982).
  89. Lipari, G., Szabo, A. Model-Free Approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules .2. Analysis of experimental results. J Am Chem Soc. 104 (17), 4559-4570 (1982).
  90. Clore, G. M., et al. Deviations from the simple two-parameter model-free approach to the interpretation of nitrogen-15 nuclear magnetic relaxation of proteins. J Am Chem Soc. 112 (12), 4989-4991 (1990).
  91. Lemaster, D. M. Larmor frequency selective model free analysis of protein NMR relaxation. J Biomol NMR. 6 (4), 366-374 (1995).
  92. Peng, J. W., Wagner, G. Mapping of spectral density functions using heteronuclear NMR relaxation measurements. J Magn Reson (1969). 98 (2), 308-332 (1992).
  93. Farrow, N. A., Zhang, O. W., FormanKay, J. D., Kay, L. E. Characterization of the backbone dynamics of folded and denatured states of an SH3 domain. Biochemistry. 36 (9), 2390-2402 (1997).
  94. Khan, S. N., et al. Distribution of pico- and nanosecond motions in disordered proteins from nuclear spin relaxation. Biophys J. 109 (5), 988-999 (2015).
  95. Smith, A. A., Ernst, M., Meier, B. H., Ferrage, F. Reducing bias in the analysis of solution-state NMR data with dynamics detectors. J Chem Phys. 151 (3), 034102 (2019).
  96. Zumpfe, K., Smith, A. A. Model-free or not. Front Mol Biosci. 8, 727553 (2021).
  97. Robustelli, P., Trbovic, N., Friesner, R. A., Palmer, A. G. Conformational dynamics of the partially disordered yeast transcription factor GCN4. J Chem Theory Comput. 9 (11), 5190-5200 (2013).
  98. Salvi, N., Abyzov, A., Blackledge, M. Multi-timescale dynamics in intrinsically disordered proteins from NMR relaxation and molecular simulation. J Phys Chem Lett. 7 (13), 2483-2489 (2016).

Reprints and Permissions

Request permission to reuse the text or figures of this JoVE article

Request Permission

Explore More Articles

NMR SpectroscopyStructural DynamicsProteins15N RelaxationGlobular ProteinsIntrinsic DisorderTROSYAtomic resolution InsightsInternal FlexibilityPicosecondsNanosecondsHetNOE ExperimentsProtein Backbone Dynamics

This article has been published

Video Coming Soon

JoVE Logo

Privacy

Terms of Use

Policies

Contact Us

Recommend to library

JoVE NEWSLETTERS

Research

Education

Authors

Librarians

ABOUT JoVE

Copyright © 2025 MyJoVE Corporation. All rights reserved