Shortly after de Broglie published his ideas that the electron in a hydrogen atom could be better thought of as being a circular standing wave instead of a particle moving in quantized circular orbits, Erwin Schrödinger extended de Broglie’s work by deriving what is now known as the Schrödinger equation. When Schrödinger applied his equation to hydrogen-like atoms, he was able to reproduce Bohr’s expression for the energy and, thus, the Rydberg formula governing hydrogen spectra. Schrödinger described electrons as three-dimensional stationary waves, or wavefunctions, represented by the Greek letter psi, ψ.
A few years later, Max Born proposed an interpretation of the wavefunction ψ that is still accepted today: Electrons are still particles, and so the waves represented by ψ are not physical waves but, instead, are complex probability amplitudes. The square of the magnitude of a wavefunction ∣ψ∣2 describes the probability of the quantum particle being present near a certain location in space. This means that wavefunctions can be used to determine the distribution of the electron’s density with respect to the nucleus in an atom. In the most general form, the Schrödinger equation can be written as:
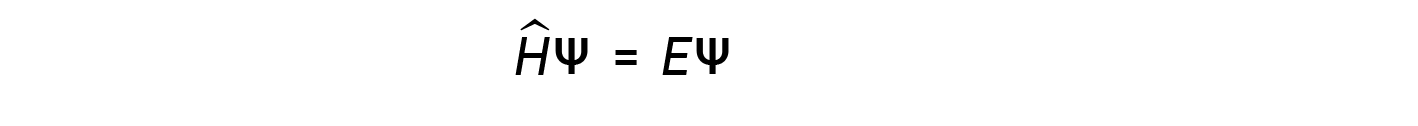
where, Ĥ is the Hamiltonian operator, a set of mathematical operations representing the total energy (potential plus kinetic) of the quantum particle (such as an electron in an atom), ψ is the wavefunction of this particle that can be used to find the special distribution of the probability of finding the particle, and E is the actual value of the total energy of the particle.
Schrödinger’s work, as well as that of Heisenberg and many other scientists following in their footsteps, is generally referred to as quantum mechanics.
The quantum mechanical model describes an orbital as a three-dimensional space around the nucleus within an atom, where the probability of finding an electron is the highest.
This text is adapted from Openstax, Chemistry 2e, Section 6.3: Development of Quantum Theory.
Du chapitre 7:

Now Playing
7.9 : The Quantum-Mechanical Model of an Atom
Electronic Structure of Atoms
41.3K Vues

7.1 : The Wave Nature of Light
Electronic Structure of Atoms
47.7K Vues

7.2 : The Electromagnetic Spectrum
Electronic Structure of Atoms
52.0K Vues

7.3 : Interference and Diffraction
Electronic Structure of Atoms
29.0K Vues

7.4 : Photoelectric Effect
Electronic Structure of Atoms
28.9K Vues

7.5 : The Bohr Model
Electronic Structure of Atoms
48.4K Vues

7.6 : Emission Spectra
Electronic Structure of Atoms
48.0K Vues

7.7 : The de Broglie Wavelength
Electronic Structure of Atoms
25.1K Vues

7.8 : The Uncertainty Principle
Electronic Structure of Atoms
22.6K Vues

7.10 : Quantum Numbers
Electronic Structure of Atoms
33.9K Vues

7.11 : Atomic Orbitals
Electronic Structure of Atoms
32.5K Vues

7.12 : The Pauli Exclusion Principle
Electronic Structure of Atoms
32.2K Vues

7.13 : The Energies of Atomic Orbitals
Electronic Structure of Atoms
23.4K Vues

7.14 : The Aufbau Principle and Hund's Rule
Electronic Structure of Atoms
40.6K Vues

7.15 : Electron Configuration of Multielectron Atoms
Electronic Structure of Atoms
36.2K Vues